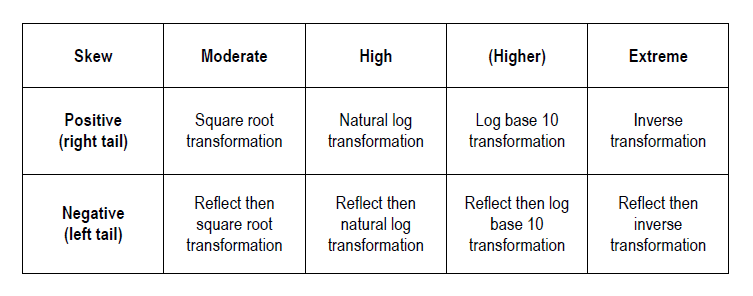
Innumerable statistical tests exist for application in hypothesis testing based on the shape and nature of the pertinent variable’s distribution. If however the intention is to perform a parametric test – such as ANOVA, Pearson’s correlation or some types of regression – the results of such a test will be more valid if the distribution of the dependent variable(s) approximates a Gaussian (normal) distribution and the assumption of homoscedasticity is met. In reality data often fails to conform to this standard, particularly in cases where the sample size is not very large. As such, data transformation can serve as a useful tool in readying data for these types of analysis by improving normality, homogeneity of variance or both.For the purposes of Transforming Skewed Data, the degree of skewness of a skewed distribution can be classified as moderate, high or extreme. Skewed data will also tend to be either positively (right) skewed with a longer tail to the right, or negatively (left) skewed with a longer tail to the left. Depending upon the degree of skewness and whether the direction of skewness is positive or negative, a different approach to transformation is often required. As a short-cut, uni-modal distributions can be roughly classified into the following transformation categories:
This article explores the transformation of a positively skewed distribution with a high degree of skewness. We will see how four of the most common transformations for skewness – square root, natural log, log to base 10, and inverse transformation – have differing degrees of impact on the distribution at hand. It should be noted that the inverse transformation is also known as the reciprocal transformation. In addition to the transformation methods offered in the table above Box-Cox transformation is also an option for positively skewed data that is >0. Further the Yeo-Johnson transformation is an extension of the Box-Cox transformation which does not require the original data values to be positive or >0.
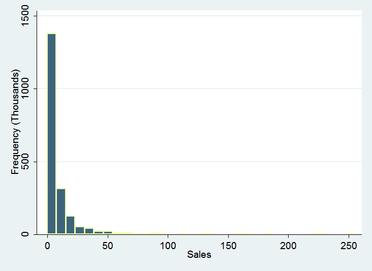
The following example takes medical device sales in thousands for a sample of 2000 diverse companies. The histogram below indicates that the original data could be classified as “high(er)” positive skewed.
The skew is in fact quite pronounced – the maximum value on the x axis extends beyond 250 (the frequency of sales volumes beyond 60 are so sparse as to make the extent of the right tail imperceptible) – it is however the highly leptokurtic distribution that that lends this variable to be better classified as high rather than extreme. It is in fact log-normal – convenient for the present demonstration. From inspection it appears that the log transformation will be the best fit in terms of normalising the distribution.
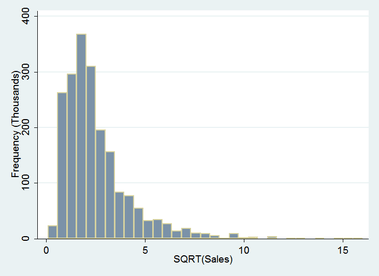
Starting with a more conservative option, the square root transformation, a major improvement in the distribution is achieved already. The extreme observations contained in the right tail are now more visible. The right tail has been pulled in considerably and a left tail has been introduced. The kurtosis of the distribution has reduced by more than two thirds.
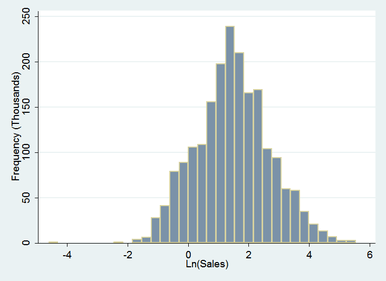
A natural log transformation proves to be an incremental improvement yielding the following results:
This is quite a good outcome – the right tail has been reduced considerably while the left tail has extended along the number line to create symmetry. The distribution now roughly approximates a normal distribution. An outlier has emerged at around -4.25, while extreme values of the right tail have been eliminated. The kurtosis has again reduced considerably.
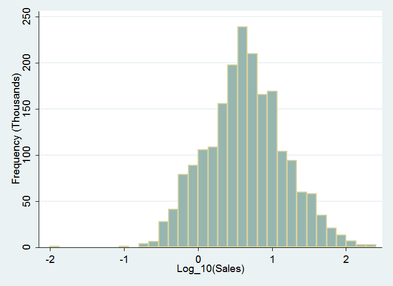
Taking things a step further and apply a log to base 10 transformation yields the following:
In this case the right tail has been pulled in even further and the left tail extended less than the previous example. Symmetry has improved and the extreme value in the left tail has been bought closer in to around -2. The log to base ten transformation has provided an ideal result – successfully transforming the log normally distributed sales data to normal.
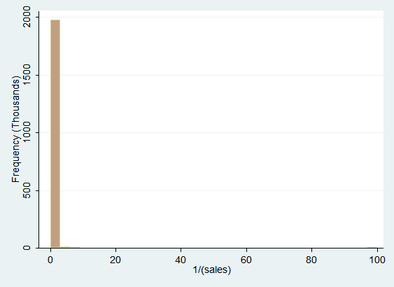
In order to illustrate what happens when a transformation that is too extreme for the data is chosen, an inverse transformation has been applied to the original sales data below.
Here we can see that the right tail of the distribution has been brought in quite considerably to the extent of increasing the kurtosis. Extreme values have been pulled in slightly but still extend sparsely out towards 100. The results of this transformation are far from desirable overall.
Some thing to note is that in this case the log transformation has caused data that was previously greater than zero to now be located on both sides of the number line. Depending upon the context, data containing zero may become problematic when interpreting or calculating the confidence intervals of un-back-transformed data. As log(1)=0, any data containing values <=1 can be made >0 by adding a constant to the original data so that the minimum raw value becomes >1 . Reporting un-back-transformed data can be fraught at the best of times so back-transformation of transformed data is recommended. Further information on back-transformation can be found here.
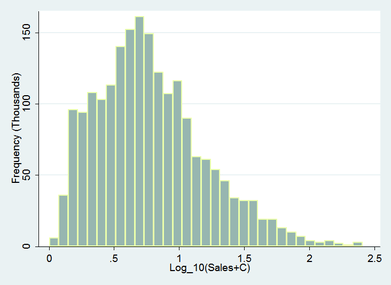
Adding a constant to data is not without it’s impact on the transformation. As the below example illustrates the effectiveness of the log transformation on the above sales data is effectively diminished in this case by the addition of a constant to the original data.
Depending on the subsequent intentions for analysis this may be the preferred outcome for your data – it is certainly an adequate improvement and has rendered the data approximately normal for most parametric testing purposes.
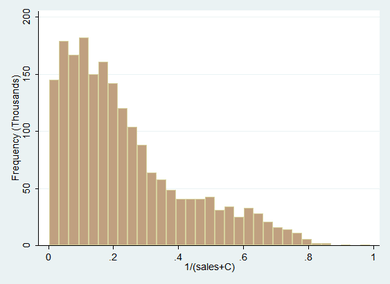
Taking the transformation a step further and applying the inverse transformation to the sales + constant data, again, leads to a less optimal result for this particular set of data – indicating that the skewness of the original data is not quite extreme enough to benefit from the inverse transformation.
It is interesting to note that the peak of the distribution has been reduced whereas an increase in leptokurtosis occurred for the inverse transformation of the raw distribution. This serves to illustrate how a small alteration in the data can completely change the outcome of a data transformation without necessarily changing the shape of the original distribution.
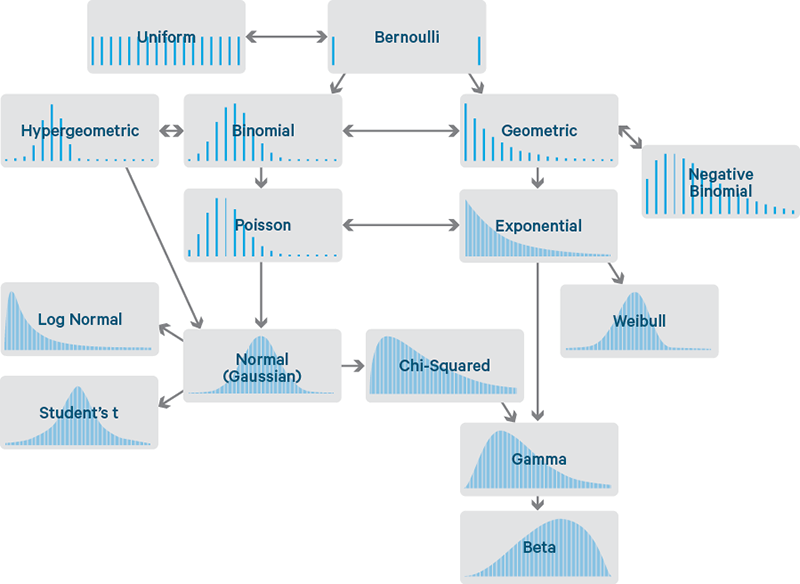
There are many varieties of distribution, the below diagram depicting only the most frequently observed. If common data transformations have not adequately ameliorated your skewness, it may be more reasonable to select a non-parametric hypothesis test that is based on an alternate distribution.
Image credit: cloudera.com

Have you ever considered about adding a little bit more than just your articles? I mean, what you say is fundamental and everything. However think about if you added some great photos or video clips to give your posts more, “pop”! Your content is excellent but with pics and clips, this blog could definitely be one of the best in its field. Good blog!
I was able to find good information from your blog articles.
hi!,I like your writing very much! percentage we keep in touch more approximately your post on AOL?
I require an expert on this space to solve my problem.
Maybe that is you! Taking a look forward to
peer you.
Great goods from you, man. I have understand your stuff previous to and you’re just extremely fantastic.
I really like what you have acquired here, certainly like what you are saying and
the way in which you say it. You make it enjoyable and you still care for to keep it
sensible. I cant wait to read much more from you. This is really
a terrific website.
Ahaa, its good discussion on the topic of this article at this place at this blog, I have read all that, so now me also commenting here.
Every weekend i used to pay a quick visit this web page, as i wish for enjoyment, since this this site conations
really good funny information too.
Oh my goodness! Impressive article dude! Many thanks, However I am encountering issues with your RSS.
I don’t understand the reason why I cannot subscribe
to it. Is there anybody else getting the same RSS problems?
Anyone that knows the answer will you kindly respond?
Thanks!!
Oh my goodness! Impressive article dude! Many thanks, However I am
going through difficulties with your RSS. I don’t understand
the reason why I can’t join it. Is there anybody
getting similar RSS issues? Anyone who knows the solution will you kindly respond?
Thanx!!
It’s a shame you don’t have a donate button! I’d definitely donate to this superb blog!
I suppose for now i’ll settle for bookmarking and adding your RSS feed
to my Google account. I look forward to new updates and will talk about this website with my Facebook group.
Chat soon!
It’s actually a great and useful piece of info. I am happy that you simply shared this helpful information with us.
Please keep us up to date like this. Thank you for
sharing.
Hey there, You’ve done an incredible job. I’ll definitely digg it and personally recommend to my friends.
I’m sure they’ll be benefited from this website.
You are so interesting! I don’t think I have read anything like this before.
So good to find somebody with genuine thoughts on this subject matter.
Seriously.. thank you for starting this up.
This site is something that’s needed on the
web, someone with a bit of originality!
Way cool! Some extremely valid points! I appreciate you
penning this post and the rest of the website is also very good.
Excellent blog here! Also your web site loads up fast!
What host are you using? Can I get your affiliate link to your host?
I wish my web site loaded up as quickly as yours lol
I like what you guys are usually up too. This sort of clever
work and exposure! Keep up the superb works guys I’ve
added you guys to my personal blogroll.
Thanks for another magnificent article. Where else could anybody get that kind of info in such an ideal way of writing? I have a presentation next week, and I’m on the look for such info.
This web site really has all of the info I wanted about this subject and didn’t know who to
ask.
Great web site. Plenty of useful info here. I am sending it to a few friends ans also sharing in delicious. And certainly, thanks for your effort!
Thanks for another wonderful article. Where else could anyone get that kind of information in such an ideal way of writing? I have a presentation next week, and I am on the look for such info.