Latent variable modelling and the chi squared exact fit statistic
Latent variable models are exploratory or confirmatory in nature in the sense that they are designed to uncover causal relationships between observable or manifest variables and corresponding latent variables in an inter-correlated data set. They use structural equation modelling (SEM) and more specifically factor analysis techniques to determine these causal relationships which and allow the testing of numerous multivariate hypotheses simultaneously. A key assumption of SEM is that the model is fully correctly specified. The reason for this is this is that one small misspecification can affect all parameter estimations in the model, rendering inaccurate approximations which can combine in unpredictable ways (3).
With any postulated statistical model it is imperative to assess and validate the model fit before concluding in favour of the integrity of the model and interpreting results. The acceptable way to do this across all structural equation models is the chi squared (χ²) statistic.
A statistically significant χ² statistic is indicative of the following:
- A systematically miss-specified model with the degree of misspecification a function of the χ² value.
- The set of parameters specified in the model do not adequately fit the data and thus that the parameter estimates of the model are inaccurate. As χ² operates on the same statistical principles as the parameter estimation, it follows that in order to trust the parameter estimates of the model we must also trust the χ², or vice versa.
- As a consequence there is a need for an investigation of where these misspecification have occurred and a potential readjustment of the model to improve its accuracy.
While one or more incorrect hypotheses may have caused the model misspecification, the misspecification could equally have resulted from other causes. It is important to thus investigate the causes of a significant model fit test . In order to properly do this the following should be evaluated:
- Heterogeneity:
- Does the causal model vary between sub groups of subjects?
- Are there any intervening within subject variables?
- Independence:
- Are the observations truly independent?
- Latent variable models involve two key assumptions: that all manifest variables are independent after controlling for any latent variables and, an individual’s position on a manifest variable is the result of that individual’s position on the corresponding latent variable (3).
- Multivariate normality:
- Is the multivariate normality assumption satisfied?
The study:
A 2015 meta-analysis of 75 latent variable studies drawn from 11 psychology journals has highlighted a tendency in clinical researchers to ignore the χ² exact fit statistic when reporting and interpreting the results of the statistical analysis of latent variable models (4).
97% of papers reported at least one appropriate model, despite the fact that 80% of these did not pass the criteria for model fit and the χ² exact fit statistic was ignored. Only 2% of overall studies concluded that the model doesn’t fit at all and one of these interpreted a model anyway (4).
Reasons for ignoring the model fit statistic: overly sensitive to sample size, penalises models when number of variables is high, general objection to the logic of exact fit hypothesis. Overall broach consensus of preference for Approximate fit indices (AFI).
AFI are instead applied in these papers to justify the models. This typically leads to questionable conclusions. In all just 41% of studies reported χ² model fit results. 40% of the studies that failed to report a p value for the reported χ² value did report a degrees of freedom. When this degrees of freedom was used to cross check the unreported p values, all non-reported p values were in fact significant.
The model fit function was usually generated through maximum likelihood methods, however 43% of studies failed to report which fit function was used.
A further tendency to accept the approximate fit hypothesis when in fact there was no or little evidence of approximate fit. This lack of thorough model examination empirical evidence of questionable validity. 30% of studies showed custom selection of more lax cut-off criteria for the approximate fit statistics than was conventionally acceptable, while 53% failed to report on cut-off criteria at all.
Assumption testing for univariate normality was assessed in only 24% of studies (4).
Further explanation of χ² and model fit:
The larger the data set the more that increasingly trivial discrepancies are detected as a source of model misspecification. This does not mean that trivial discrepancies become more important to the model fit calculation, it means that the level of certainty with which these discrepancies can be considered important has increased. In other words, the statistical power has increased. Model misspecification can be the result of both theoretically relevant and irrelevant/peripheral causal factors which both need to be equally addressed. A significant model fit statistic indicating model misspecification is not trivial just because the causes of the misspecification are trivial. It is instead the case that trivial causes are having a significant effect and thus there is a significant need for them to be addressed. The χ² model fit test is the most sensitive way to detect misspecification in latent variable models and should be adhered to above other methods even when sample size is high. In the structural equation modelling context of multiple hypotheses, a rejection of model fit does not result in the necessary rejection of each of the models hypotheses (4).
Problems with AFI:
The AFI statistic does provide a conceptually heterogeneous set of fit indices for each hypothesis, however none of these indices are accompanied by a critical value or significance level and all except one arise from unknown distributions. The fit indices are a function of χ² but unlike the χ² fit statistic they do not have a verified statistical basis nor do they present a statistically rigorous test of model fit. Despite this satisfactory AFI values across hypotheses are being used to justify the invalidity of a significant χ² test.
Mote Carlo simulations of AFI concluded that it is not possible to determine universal cut off criteria in any forms of model tested. Using AFI, the probability of correctly rejecting a mis-specified model decreased with increasing sample size. This is the inverse of the statistic. Another problem with AFI compared to χ² is that the more severe the model misspecification or correlated errors, the more unpredictable the AFI become. Again this is the inverse of what happens with the χ² statistic (4).
The take away:
Based on the meta-analysis the following best practice principles are recommended in addition to adequate attention to the statistical assumptions of heterogeneity, independence and multivariate normality outlined above:
- Pay attention to distributional assumptions.
- Have a theoretical justification for your model.
- Avoid post hoc model modifications such as dropping indicators, allowing cross-loadings and correlated error terms.
- Avoid confirmation bias.
- Use an adequate estimation method.
- Recognise the existence of equivalence models.
- Justify causal inferences.
- Use clear reporting that is not selective.
Image:
Michael Eid, Tanja Kutscher, Stability of Happiness, 2014 Chapter 13 – Statistical Models for Analyzing Stability and Change in Happiness
https://www.sciencedirect.com/science/article/pii/B9780124114784000138
References:
(1). Latent Variables in Psychology and the Social Sciences
(2) Structural equation modelling and its application to network analysis in functional brain imaging
https://onlinelibrary.wiley.com/doi/abs/10.1002/hbm.460020104
(3) Chapter 7: Assumptions in Structural Equation modelling
https://psycnet.apa.org/record/2012-16551-007
(4) A cautionary note on testing latent variable models
https://www.frontiersin.org/articles/10.3389/fpsyg.2015.01715/full


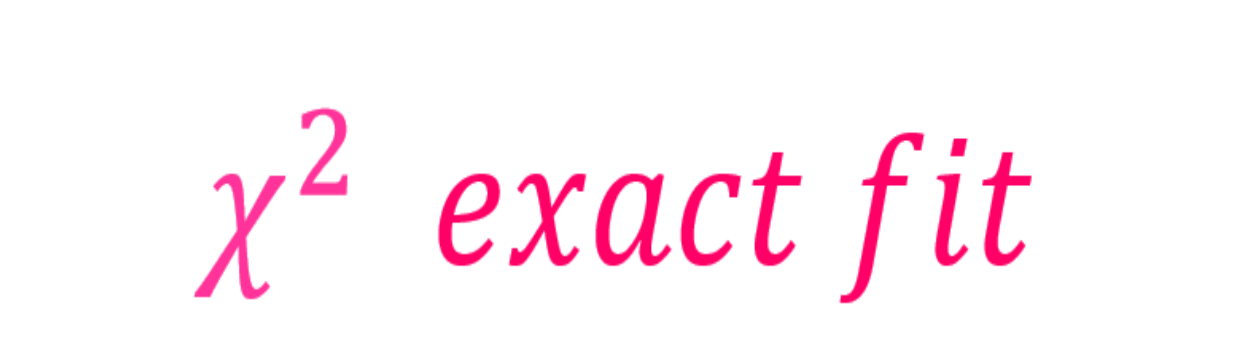
Really Great article, Amazing Write Up, I can agree with your point of view. Much appreciation for the information, Really interesting article, It’s well-structured and has good visual description, I would like to thank you for putting the time together to construct this article. It gave me a lot of information that I really enjoyed reading.