Simpson’s Paradox: the perils of hidden bias.
How Simpson’s Paradox Confounds Research Findings And Why Knowing Which Groups To Segment By Can Reverse Study Findings By Eliminating Bias.
Introduction
The misinterpretation of statistics or even the “mis”-analysis of data can occur for a variety of reasons and to a variety of ends. This article will focus on one such phenomenon contributing to the drawing of faulty conclusion from data – Simpson’s Paradox.
At times a situation arises where the outcomes of a clinical research study depict the inverse of expected (or essentially correct) outcomes. Depending upon the statistical approach, this could affect means, proportions or relational trends among other statistics.
Some examples of this occurrence are a negative difference when a positive difference was anticipated, a positive trend when a negative one would have been more intuitive – or vice versa. Another example commonly pertains to the cross tabulation of proportions, where condition A is proportionally greater over all, yet when stratified by a third variable, condition B is greater in all cases . All of these examples can be said to be instances of Simpson’s paradox. Essentially Simpson’s paradox represents the possibility of supporting opposing hypotheses – with the same data. Simpson’s paradox can be said to occur due to the effects of confounding, where a confounding variable is characterised by being related to both the independent variable and the outcome variable, and unevenly distributed across levels of the independent variable. Simpson’s paradox can also occur without confounding in the context of non-collapsability. For more information on the nuances of confounding versus non-collapsability in the context of Simpson’s paradox, see here.
In a sense, Simpson’s paradox is merely an apparent paradox, and can be more accurately described as a form of bias. This bias most often results from a lack of insight into how an unknown lurking variable, so to speak, is impacting upon the relationship between two variables of interest. Simpson’s paradox highlights the fact that taking data at face value and utilising it to inform clinical decision making can often be highly misleading. The chances of Simpson’s paradox (or bias) impacting the statistical analysis can be greatly reduced in many cases by a careful approach that has been informed by proper knowledge of the subject matter. This highlights the benefit of close collaboration between researcher and statistician in informing an optimal statistical methodology that can be adapted on a per case basis.
The following three part series explores hypothetical clinical research scenarios in which Simpson’s paradox can manifest.
Part 1
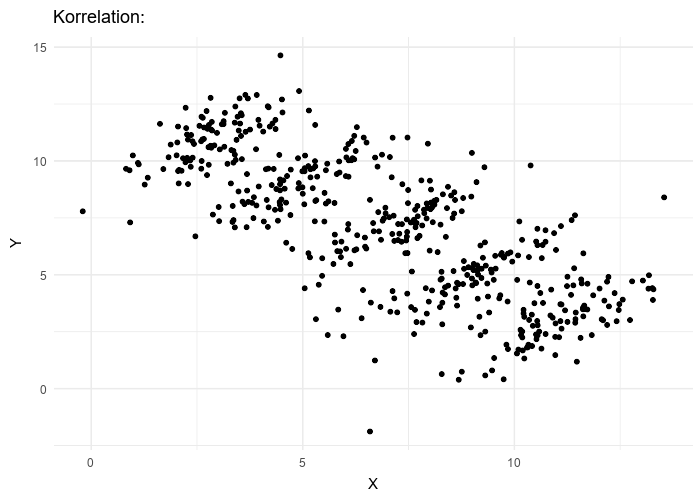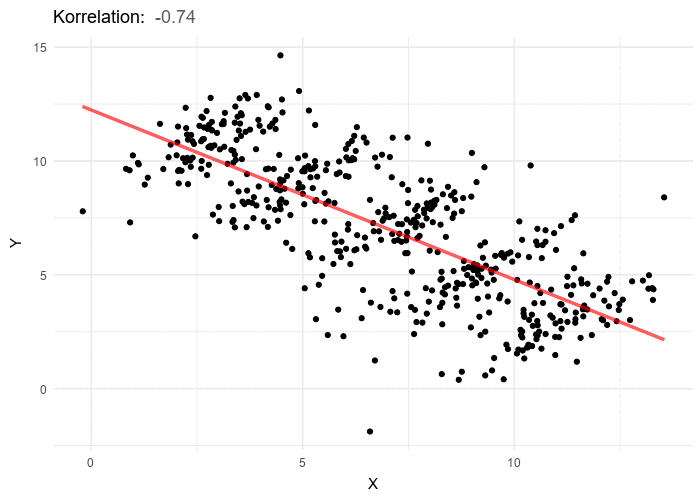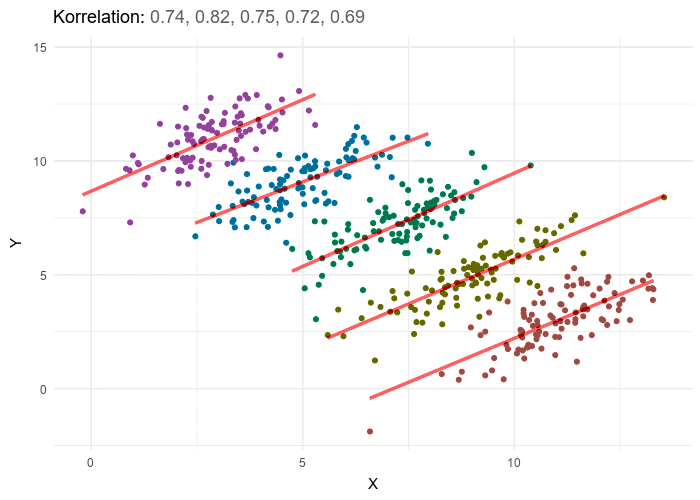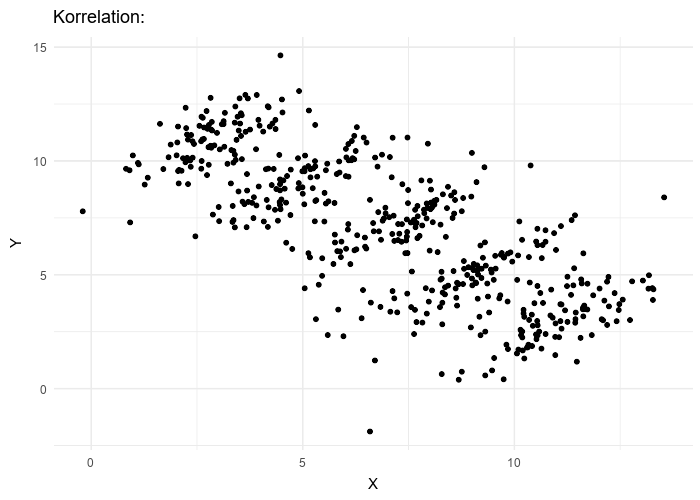
Simpson’s Paradox in correlation and linear regression
Scenario and Example
A nutritionist would like to investigate the relationships between diet and negative health outcomes. As higher weight has been previously associated with negative health outcomes, the research sets out to investigate the extent to which increased caloric intake contributes to weight gain. In researching the relationship between calorie intake and weight gain for a particular dietary regime, the nutritionist uncovers a rather unanticipated negative trend. As caloric intake increases the weight of participants appears to go down. The nutritionist therefore starts recommending higher calorie intake as a way to dramatically lose weight. Weight does appear to go down with calorie intake, however if we stratify the data by different age groupings, a positive trend between weight and calorie intake emerges for each age group. While overall elderly have the lowest calorie intake, they also have the highest weight, and teens have the highest calorie intake but the lowest weight, this accounts for the negative trend but does not give an honest picture of the impact of calories on weight. In order to gain an accurate picture of the relationship between weight and calorie intake we have to know which variable to group or stratify the data by, and in this case it’s age. Once the data is stratified by five separate age categories a positive trend between calories and weight emerges in each of the 5 categories. In general, the answer to which variable to stratify by or control for isn’t typically this obvious and in most cases and requires some theoretical background and a thorough examination of the available data including associated variables for which the information is at hand.
Remedy
In the above example, age shows a negative relationship to the independent variable, calories, but a positive relationship to the dependent variable, weight. It is for this reason that a bit of data exploration and assumption checking before any hypothesis testing is so essential. Even with these practices in place it is possible to overlook the source of confounding and caution is always encouraged.
Randomisation and Stratification:
In the context of a randomised controlled trial (RTC), the data should be randomly assigned to treatment groups as well as stratified by any pertinent demographic and other factors so that these are evenly distributed across treatment arms (levels of the independent variable). This approach can help to minimise, although not eliminate the chances of bias occurring in any such statistical context, predictive modelling or otherwise.
Linear Structural Equation Modelling:
If the data at hand is not randomised but observational, a different approach should be taken to detect causal effects in light of potential confounding or non-collapsability. One such approach is linear structural equation modelling where each variable is generated as a linear function of it’s parents, using a directed acyclic graph (DAG) with weighted edges. This is a more sophisticated and ideal approach to simply adjusting for x number of variables, which is needed in the absence of a randomisation protocol.
Heirachical regression:
This example illustrated an apparent negative trend of the overall data masking a positive trend In each individual subgroup, in practice, the reverse can also occur.
In order to avoid drawing misguided conclusion from the data the correct statistical approach must be entertained, a hierarchical regression controlling for a number of potential confounding factors could avoid drawing wrong conclusion due to Simpson’s paradox.
Article: Sarah Seppelt Baker
Reference:
The Simpson’s paradox unraveled, Hernan, M, Clayton, D, Keiding, N., International Journal of Epidemiology, 2011.
Part 2
Simpson’s Paradox in 2 x 2 tables and proportions
Scenario and Example
Simpson’s paradox can manifest itself in the analysis of proportional data and two by two tables. In the following example two pharmaceutical cancer treatments are compared by a drug company utilising a randomised controlled clinical trial design. The company wants to test how the new drug (A) compares to the standard drug (B) already widely in clinical use. 1000 patients were randomly allocated to each group. A chi squared test of remission rates between the two drug treatments is highly statistically significant, indicating that the new drug A is the more effective choice. At first glance this seems reasonable, the sample size is fairly large and equal number of patients have been allocated to each groups.
Drug Treatment | A | B |
Remisson Yes | 798 (79.8%) | 705 (70.5%) |
Remission No | 202 | 295 |
Total sample size | 1000 | 1000 |
When we take a closer look, the picture changes. It turns out the clinical trial team forgot to take into account the patients stage of disease progression at the commencement of treatment. The table below shown that drug A was allocated to far more patients with stage II cancer (79.2%) and drug B was allocated to far more patients with stage IV cancer (79.8%).
| Stage II | Stage IV | ||
Drug Treatment | A | B | A | B |
Remission Yes | 697 (87.1%) | 195 (92.9%) | 101 (50.5%) | 510 (64.6%) |
Remission No | 103 | 15 | 99 | 280 |
Total sample size | 800 | 210 | 200 | 790 |
The chi-square statistic for the difference in remission rates between treatment groups for patients with stage IV disease progression at treatment outset is 13.3473. The p-value is .000259. The result is significant at p < .05.
Unfortunately the analysis of tabulated data is no less prone to bias in results akin to Simpson’s Paradox than continuous data. Given that stage II cancer is easier to treat than stage IV, this has given drug A an unfair advantage and has naturally lead to a higher remission rate overall for drug A. When the treatment groups are divided by disease progression categories and reanalysed, we can see that remission rates are higher for drug B in both stage II and stage IV baseline disease progression. The resulting chi squared statistics are wildly different to the first and statistically significant in the opposite direction to the first analysis. In causal terms, stage of disease progression affects difficulty of treatment and likelihood of remission. Patients at a more advanced stage of disease, ie stage IV, will be harder to treat than patients at stage II. In order for a fair comparison between two treatments, patients stage of disease progression needs to be taken into account. In addition to this some drugs may be more efficacious at one stage or the other, independent of the overall probabilities of achieving remission at either stage.
Remedy
Randomisation and Stratification:
Of course in this scenario, stage of disease progression is not the only variable that needs to be accounted for in order to insure against biased results. Demographic variables such as age, sex socio-economic status and geographic location are some examples of variables that should be controlled for in any similar analysis. As with the scenario in part 1, this can be achieved is through stratified random allocation of patients to treatment groups at the outset of the study. Using a randomised controlled trial design where subjects are randomly allocated to each treatment group as well as stratified by pertinent demographic and diagnostic variables will reduce the chances of inaccurate study results occurring due to bias.
Further examples of Simpson’s Paradox in 2 x 2 tables
Simpson’s paradox in case control and cohort studies
Case control and cohort studies also involve analyses which rely on the 2×2 table. The calculation of their corresponding measures of association the odds ratio and relative risk, respectively, is unsurprisingly not immune to the effect of bias and in much the same way as the chi square example above. This time, a reversed odds ratio or relative risk in the opposite direction can occur if the pertinent bias has not been accounted and controlled for.
Simpson’s paradox in meta-analysis of case control studies
Following on from the example above, this form of bias can pose further problems in the context of meta-analysis. When combining results from numerous case control studies the confounders in question may or may not have been identified or controlled for consistently across all studies and some studies will likely have identified different confounders to the same variable of interest. The odds ratios produced by the different studies can therefore be incompatible and lead to erroneous conclusions. Meta-analysis can therefore fall prey to ecological fallacy as a result of systematic bias, where the odds ratio for the combined studies is in the opposite direction to the odds ratios of the separate studies. Imbalance in treatment arm size has also been found to act as a confounder in the context of meta-analysis of randomised controlled trials. Other methodological differences between studies may also be at play, such as differences in follow-up times between studies or a very low proportion of observed events occurring in some studies, potentially due to a shorted follow-up time.
That’s not to say that meta-analysis cannot be performed on these studies, inter-study variation is of-course more common than not, as with all other analytical contexts it is necessary to proceed with a high level of caution and attention to detail. On the whole an approach of simply pooling study results is not reliable, the use of more sophisticated meta-analytic techniques, such as random effects models or Bayesian random effects models that use a Markov chain algorithm for estimating the posterior distributions, are required to mitigate inherent limitations of the meta-analytic approach. Random-effects models assume the presence of study-specific variance which is a latent variable to be partitioned. Bayesian random-effects models can come in parametric, non-parametric or semi-parametric varieties, referring to the shape of the distributions of study-specific effects.
For more information on Simpson’s paradox in meta-analysis, see here.
https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/1471-2288-8-34
For more information on how to minimise bias in meta-analysis, see here.
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3868184/
https://onlinelibrary.wiley.com/doi/abs/10.1002/sim.4780110202
Simpson’s Paradox & Cox Proportional Hazard Models
Scenario and example
A 2017 paper describes a scenario whereby the death rate due to tuberculosis was lower in Richmond than New York for both African-Americans and for Caucasian-Americans, yet lower in New York than Richmond when the two ethnic groups were combined.
For more details on this example as well as the mathematics behind it see here.
For more examples of Simpson’s paradox in Cox regression see here.
Factors contributing to bias in survival models can be different to those in more straightforward contexts. Many clinical and epidemiological studies include data from multiple sites. More often than not there is heterogeneity across sites. This heterogeneity can come is various forms and can result in within and between–site clustering, or correlation, of observations on site specific variables. This clustering, if not controlled for, can lead to Simpson’s paradox in the form of hazard rate reversal, across some or all of time T, and has been found to be a common explanation of the phenomenon in this context. Site clustering can occur on the patient level, for example, due to site specific selection procedures for the recruitment of patients (lead by the principal investigators individual to each site), or differences in site specific treatment protocols. Site specific differences can occur intra or internationally and in the international case can be due, for example, to differences in national treatment guidelines or differences in drug availability between countries. Resource availability can also differ between sites whether intra or internationally. In any time to event analysis involving multiple sites (such as the Cox regression model) a site-level effect should be taken into account and controlled for in order to avoid bias-related inferential errors.
Remedy
Cox regression Model including site as a fixed covariate:
Site should be included as a covariate in order to account for site specific dependence of observations.
Cox regression Model treating site as a stratification variable:
In cases where one or more covariates violate the Proportional Hazards (PH) assumption as indicated by a lack of independence of scaled Schonefeld residuals to time, stratification may be more appropriate. Another option in this case is to add a time-varying covariate to the model. The choice made in this regard will depend on the sampling nuances of each particular study.
Cox shared frailty model:
In specific conditions the Cox shared frailty model may be more appropriate. This approach involves treating subjects from the same site as having the same frailty and requires that each subjects is not clustered across more than one level two unit. While it is not appropriate for multi-membership multi-level data, it can be useful for more straight forward scenarios.
In tailoring the approach to the specifics of the data, appropriate model adjustments should produce hazard ratios that more accurately estimate the true risk.